|
Feature: Calculating Pi
Posted by Nick on 14 March 2000, 03:57 GMT
I hope everyone is having a very happy Pi Day! In case you don't know, today (March 14) is Pi Day. In honor of this, this week's feature will be in homage of our favorite irrational number. Andy Selle has written us a feature regarding pi and its origins. Check out the updated version instead. It is available in PDF or HTML
Calculating  : an explorative tour : an explorative tour Andrew Selle (aselle@ticalc.org)
Abstract: A look at calculating 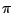 with a TI graphing calculator. This article goes through a variety of methods for finding the ever closer decimal approximation of our favorite trancendental number.
Introduction 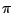 is a very interesting number. We are first introduced to it early in our grade-schooling as a component of the formulas is a very interesting number. We are first introduced to it early in our grade-schooling as a component of the formulas 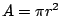 and and 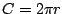 . It seems odd to us that we need to use this number. Where did it come from? How did we ever figure it out? These our questions that I hope to address and perhaps answer. However, the major point of this article is to explore methods of calculating . It seems odd to us that we need to use this number. Where did it come from? How did we ever figure it out? These our questions that I hope to address and perhaps answer. However, the major point of this article is to explore methods of calculating 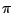 using a Texas Instruments graphing calculator (and perhaps a few computers). using a Texas Instruments graphing calculator (and perhaps a few computers).
History The history of 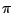 is a long one. The first significant advancement in the understanding of is a long one. The first significant advancement in the understanding of 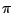 was the Ancient Greeks. They came up with the concept of inscribing a polygon inside a circle. As you added more sides to the polygon, the polygon became closer and closer to a circle. By taking the ratio between the polygon's area to the circle's area, you could find was the Ancient Greeks. They came up with the concept of inscribing a polygon inside a circle. As you added more sides to the polygon, the polygon became closer and closer to a circle. By taking the ratio between the polygon's area to the circle's area, you could find 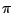 Thus, the first method of calculating Thus, the first method of calculating 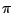 was born. was born.
During the middle ages, time for calculating 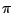 was not readily available. Even when it was, the polygon inscribing method was very slow and painstaking. It was eventually discovered that an infinite series approximating was not readily available. Even when it was, the polygon inscribing method was very slow and painstaking. It was eventually discovered that an infinite series approximating 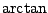 was a good means to calculate was a good means to calculate 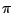 . Once the computer was invented, . Once the computer was invented, 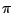 was quickly calculated to many places. was quickly calculated to many places.
This history is in no way complete, but it covers the major ideas.
Math Obviously, a lot of math is involved in calculating 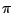 . I will derive all my mathematics as completely as possible, but don't be afraid to skip the derivations if you are not interested. I will highlight the important results found to make this easy. . I will derive all my mathematics as completely as possible, but don't be afraid to skip the derivations if you are not interested. I will highlight the important results found to make this easy. Monte Carlo Method Derivation One of my favorite methods, and one of the simplest to understand is the Monte Carlo method. I first ran into this method when I was learning BASIC for my Apple II. One sets up a square that is 2 by 2. One then inscribes a circle inside the square. Random points are then plotted repeatedly. For each point we add one to the variable n, and if the point is within the circle we add one to the variable i. Then to calculate we simply put together what we know. 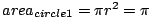 ,areasquare = 4. Now, we can setup the proportion ,areasquare = 4. Now, we can setup the proportion 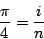 . Thus, . Thus, 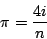 Implementation This program can be easily implemented in 8x TI-BASIC as: :0 --> N0 --> D
:While 1
:rand*2-1 --> X
:rand*2-1 --> Y
:If sqrt(x^2+y^2)=< 1
:N+1 --> N
:End
:D+1 --> D
:Disp (N/D*4)
:End
Bibliography 1) Dara Hazeghi: Dara's Pi Page http://www.geocities.com/EnchantedForest/5815/,
Accessed 3/4/2000
2) JOC/EFR: Pi Through the Ages http://www-groups.dcs.st-and.ac.uk/
If you don't yet know how to celebrate Pi Day, here's a few tips: - Watch the movie Pi. It was written rather recently, and it's a bit artsy, but I love it. I'm planning on watching it with friends during the evening.
- Serve pie to your classes, or if you don't have enough pie, have it for dinner!
- Be psychotic like me and memorize sixty digits of pi. :)
Best wishes to you during this Pi Day season.
|
|
|
|
|
The comments below are written by ticalc.org visitors. Their views are not necessarily those of ticalc.org, and ticalc.org takes no responsibility for their content.
|
|
|
Re: Feature: Calculating Pi
|
brentes
(Web Page)
|
|
I am going to tell all of you this just FYI.
My search pi script is now DOWN because I got a message from my Server Administrator saying it took up an unbelievable amount of cpu from their machines or something. After all, it was on slashdot :)
sorry for the inconveniance :)
|
|
|
14 March 2000, 17:57 GMT
|
|
|
Re: Feature: Calculating Pi
|
Nathan Walters 
|
|
Happy Pi Time!!! in Eastern time, it is 3/14, at 1:59 and 26.5 seconds approxamately.
i hurried home from school to make it! :-) sorry i can't make it more exact, but it takes time to post this message, and different clocks are going to show slightly different times.
nathan (by the way, Yes, i do need a life)
|
|
|
14 March 2000, 19:58 GMT
|
|
|
A few more tidbits
|
Grant Elliott 
(Web Page)
|
|
My favorite formula for pi:
lim (as n approaches infinity) sin(180/n)*cos(180/n)*n
This is the easiest to derive. The area of a regular polygon with n sides and radius R is:
sin(180/n)*cos(180/n)*n*R^2
And since the area of a regular polygon with infinite sides is pi*R^2 (we can prove that it is directly proportional to R^2), we obtain that pi is equal to the above limit.
Of course, this formula is useless if the algorithm you use for sin and cos uses pi. But there are plenty that don't.
On another fun note, I'll now list off a few other fun tricks with transidential numbers and other fun stuff:
The nth Fibonacci number is (phi^n-psi^n)/sqrt(n)
e^(pi*i) = -1
i^i = e^(-pi*i/2)
tau(tau(15!)) = 42
My favorite is the last one : )
On a final note, you can't appreciate pi until you read The Joy of Pi. You can enjoy some of the fun at www.joyofpi.com The book has all sorts of fun things. Among them are the first 1,000,000 digits of pi printed in the background on every page. (You can find 10,000 at the webpage.) Better still,
important digits are marked. Ever wonder what the 3rd digit of pi is? What about the 31st? 314th? 3141st? 31415th?
And, of course, the most important digit: THE 42nd DIGIT OF PI : ) I looked it up once. I think it's a 9.
Why didn't ticalc celebrate e day? What about phi day? Why not celebrate the 42nd day of the year?
This concludes yet another edition of "Grant Babbles meaninglessly."
|
|
|
14 March 2000, 22:21 GMT
|
|
|
Re: Feature: Calculating Pi
|
Garrett Cradduck 
(Web Page)
|
|
Alright...apparently(as far as I can tell) no one's seen fit to mention another method of
calculating grand ol' pi, so here it is:
1/1 +1/4 +1/9 +1/16 +1/25 +1/36 + ....... = [(pi)^2]/6.
Bernoulli never managed to find this exact answer, so it was left to
Euler, whom you can thank for the above equality.
I don't suggest using this to calculate pi, though, as convergence
is absolutely horrendous. Just thought I'd throw it out there.
|
|
|
14 March 2000, 22:32 GMT
|
|
|
Re: Feature: Calculating Pi
|
S B 
|
|
You know that if you are realy inclined to do the calculations (or the aproxamate 22/7). you could calculate it on the calculator in your computer (or just press the frigging pi key).
|
|
|
14 March 2000, 23:31 GMT
|
|
|
Re: Feature: Calculating Pi
|
damian Ancukiewicz 
(Web Page)
|
|
I memorized 66 digits of pi about a year ago:
3.141592 6535897932 38462643383 27950 2884197169 399375105
Whenever I recite it people think i'm crazy.
Maybe i am...
|
|
|
15 March 2000, 02:45 GMT
|
|
|
Re: Feature: Calculating Pi
|
|
Spoon_Man
|
|
I know this is off subject but could someone please email me info on how to downgrade from AMS 2.03 to 1.0x, thank you
Ps. I have an H1 Ti-89
|
|
|
15 March 2000, 03:12 GMT
|
|
|
Program for Pi
|
Wolf 
(Web Page)
|
|
Those are all good programs on the top, but they take too long, and don't give the right answers, not right enough. Here is a program that is easier, faster, and gets the right answer. It's different, without the "circle" graphic, but I think it's better this way.
The " ' " in the code mean commenting, don't type that in
Program:Pi
Degree 'sets the mode for degrees, otherwise all screwed up
0->d 'clears values
2->x 'clears values
While 1 'starts an endless loop
x+1->x 'increases number of verteces on the figure
(x*sin ((360/x)/2)))+x*(tan((360/x)/2))->N 'calculates the value
n/2->d 'stores the value
Disp d 'outputs the actual value
' Disp x ' put this to tell you at what point the value comes really close to Pi
End 'says where the loop goes to the beginning
Hope you're happy this way. Visit the website, and write me back, any flames welcome.
|
|
|
15 March 2000, 06:09 GMT
|
|
 |
 |
 |
|
Re: Program for Pi
|
Wolf 
(Web Page)
|
|
By the way, the program puts a figure with an n number of verteces both inside AND outside the figure, finds the perimeter of both, and then averages, this is exact, but REALLY needs a high number of verteces, in the order of five THOUSAND. I'll be putting the program on my website, plus program to calculate e, all for the TI-86/85. have fun, and happy coding!
|
|
|
15 March 2000, 15:58 GMT
|
|
1 2 3 4 5 6 7
You can change the number of comments per page in Account Preferences.
|

