|
Feature: Calculating Pi
Posted by Nick on 14 March 2000, 03:57 GMT
I hope everyone is having a very happy Pi Day! In case you don't know, today (March 14) is Pi Day. In honor of this, this week's feature will be in homage of our favorite irrational number. Andy Selle has written us a feature regarding pi and its origins. Check out the updated version instead. It is available in PDF or HTML
Calculating  : an explorative tour : an explorative tour Andrew Selle (aselle@ticalc.org)
Abstract: A look at calculating 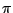 with a TI graphing calculator. This article goes through a variety of methods for finding the ever closer decimal approximation of our favorite trancendental number.
Introduction 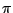 is a very interesting number. We are first introduced to it early in our grade-schooling as a component of the formulas is a very interesting number. We are first introduced to it early in our grade-schooling as a component of the formulas 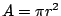 and and 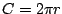 . It seems odd to us that we need to use this number. Where did it come from? How did we ever figure it out? These our questions that I hope to address and perhaps answer. However, the major point of this article is to explore methods of calculating . It seems odd to us that we need to use this number. Where did it come from? How did we ever figure it out? These our questions that I hope to address and perhaps answer. However, the major point of this article is to explore methods of calculating  using a Texas Instruments graphing calculator (and perhaps a few computers). using a Texas Instruments graphing calculator (and perhaps a few computers).
History The history of  is a long one. The first significant advancement in the understanding of is a long one. The first significant advancement in the understanding of  was the Ancient Greeks. They came up with the concept of inscribing a polygon inside a circle. As you added more sides to the polygon, the polygon became closer and closer to a circle. By taking the ratio between the polygon's area to the circle's area, you could find was the Ancient Greeks. They came up with the concept of inscribing a polygon inside a circle. As you added more sides to the polygon, the polygon became closer and closer to a circle. By taking the ratio between the polygon's area to the circle's area, you could find 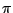 Thus, the first method of calculating Thus, the first method of calculating 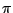 was born. was born.
During the middle ages, time for calculating 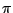 was not readily available. Even when it was, the polygon inscribing method was very slow and painstaking. It was eventually discovered that an infinite series approximating was not readily available. Even when it was, the polygon inscribing method was very slow and painstaking. It was eventually discovered that an infinite series approximating 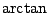 was a good means to calculate was a good means to calculate 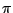 . Once the computer was invented, . Once the computer was invented, 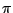 was quickly calculated to many places. was quickly calculated to many places.
This history is in no way complete, but it covers the major ideas.
Math Obviously, a lot of math is involved in calculating 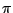 . I will derive all my mathematics as completely as possible, but don't be afraid to skip the derivations if you are not interested. I will highlight the important results found to make this easy. . I will derive all my mathematics as completely as possible, but don't be afraid to skip the derivations if you are not interested. I will highlight the important results found to make this easy. Monte Carlo Method Derivation One of my favorite methods, and one of the simplest to understand is the Monte Carlo method. I first ran into this method when I was learning BASIC for my Apple II. One sets up a square that is 2 by 2. One then inscribes a circle inside the square. Random points are then plotted repeatedly. For each point we add one to the variable n, and if the point is within the circle we add one to the variable i. Then to calculate we simply put together what we know. 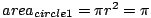 ,areasquare = 4. Now, we can setup the proportion ,areasquare = 4. Now, we can setup the proportion 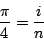 . Thus, . Thus, 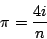 Implementation This program can be easily implemented in 8x TI-BASIC as: :0 --> N0 --> D
:While 1
:rand*2-1 --> X
:rand*2-1 --> Y
:If sqrt(x^2+y^2)=< 1
:N+1 --> N
:End
:D+1 --> D
:Disp (N/D*4)
:End
Bibliography 1) Dara Hazeghi: Dara's Pi Page http://www.geocities.com/EnchantedForest/5815/,
Accessed 3/4/2000
2) JOC/EFR: Pi Through the Ages http://www-groups.dcs.st-and.ac.uk/
If you don't yet know how to celebrate Pi Day, here's a few tips: - Watch the movie Pi. It was written rather recently, and it's a bit artsy, but I love it. I'm planning on watching it with friends during the evening.
- Serve pie to your classes, or if you don't have enough pie, have it for dinner!
- Be psychotic like me and memorize sixty digits of pi. :)
Best wishes to you during this Pi Day season.
|
|
|
|
|
The comments below are written by ticalc.org visitors. Their views are not necessarily those of ticalc.org, and ticalc.org takes no responsibility for their content.
|
|
|
Re: Feature: Calculating Pi
|
MicroLITH 
|
|
Is someone with a Pi face someone with an incalculable number of wrinkles?
Happy Pi day.
>|
|
|
|
14 March 2000, 04:11 GMT
|
|
|
Re: Feature: Calculating Pi
|
natefanaro 
(Web Page)
|
|
I have seen the movie Pi and I thought it was interesting, though I would have liked to see it in color. I saw it a while ago so I kins of forgot how Pi had something to do with predicting the stock market. Well, maybe a sequel will come around. As for an unrelated, yet related, issue. My birthday is on Pi day. I didn't realize it untill last year though. I think I might try to get a pie that says happy birthday on it.
|
|
|
14 March 2000, 04:24 GMT
|
|
|
Re: Feature: Calculating Pi
|
Mike Knapp 
(Web Page)
|
|
Nowhere in this article did i actually see the decimal approximation of pi, so without further hesitation, I give you the first 50 decimal places of pi (recited from memory):
3.1415926535 8979323846 2643383279 5028841971 6939937501
|
|
|
14 March 2000, 04:32 GMT
|
|
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |

 |
|
Re: Re: Re: Re: Re: Feature: Calculating Pi
|
Nick Chaves 
(Web Page)
|
|
Sorry, but you're pretty ignorant. I memorized the first 60 digits, it's not that hard. I have a pretty good memory (not amazing like the people who memorized 42,000 digits, and yes, something like that is the world record. It took the guy several hours to repeat it. What a waste of time) and anyway, all I did was memorize the first few digits in patterns, and then in groups of 5s it's not that hard. 60, 70, 80 digits, whatever, is not inconveivable. It starts to get hard to believe when you talk 100s, 1000s and 10s of thousands of digits.
Nick
P.S. I admit, you cannot believe that someone "recited" those digits of pi onto a message board, therefore I am not going to. But 50+ digits is not impossible, believe me.
|
|
|
15 March 2000, 07:04 GMT
|
|
1 2 3 4 5 6 7
You can change the number of comments per page in Account Preferences.
|

